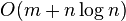- 동적 계획법
- Top-down
1. 문제를 작은 문제로 나눈다.
2. 작은 문제를 푼다.
3. 작은 문제를 풀고, 문제를 푼다.(큰 문제를 풀어 간다.)
* CODE - 피보나치
: 트리로 생각하자int memo[100]; int fibonacci(int n) { if (n <= 1) { return n; } else { memo[n] = fibonacci(n - 1) + fibonacci(n - 2); return memo[n]; } }: memorization을 이용하면 반복을 줄일 수 있다!
int memo[100]; int fibonacci(int n) { if (n <= 1) { return n; } else { if (memo[n]) { return memo[n]; } memo[n] = fibonacci(n - 1) + fibonacci(n - 2); return memo[n]; } }
- Bottom-up
1. 문제를 크기가 작은 문제부터 차례대로 푼다.
2. 문제의 크기를 조금씩 크게 만들면서 문제를 점점 푼다.
3. 작은 문제를 풀면서 왔기 때문에, 큰 문제는 항상 풀 수 있다.
4. 반복하면 언젠간 풀어야 하는 문제를 풀 수 있다.
* CODE - 피보나치int dp[100]; int fibonacci(int n) { dp[0] = 1; dp[1] = 1; for (int i = 2; i <= n; i++) { dp[i] = dp[i - 1] + dp[i - 2]; } return dp[n]; }
'Algorithm' 카테고리의 다른 글
| 에라토스테네스의체 (0) | 2016.03.22 |
|---|---|
| 알고리즘 - 보간 탐색 (0) | 2015.11.14 |
| 알고리즘 - 이진 탐색 (0) | 2015.11.14 |
| 알고리즘 - 순차 탐색 (1) | 2015.11.14 |
| 알고리즘 - 위상 정렬 (0) | 2015.11.14 |